Extraordinary advances in sequencing technology in the past decade have revolutionized biology and medicine. Many high-throughput sequencing based assays have been designed to make various biological measurements of interest. Specific problems we will study include genome assembly, haplotype phasing, RNA-Seq quantification, and single-cell RNA-Seq analysis.
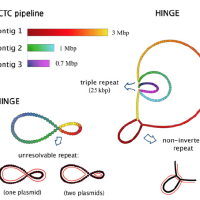
The most important problem in computational genomics is that of genome assembly. In brief, every cell of every organism has a genome, which can be thought as a long string of A, C, G, and T. With current technology we do not have the ability to read the entire genomes, but get random noisy sub-sequences of the genome called reads. The genome assembly problem is to reconstruct the genome from these reads. We study the fundamental limits of this problem and design scalable algorithms for this.
We considered this problem and firstly studied fundamental limits for being able to reconstruct the genome perfectly. However, we found that the conditions that were derived here to be able to recover uniquely were not satisfied in most practical datasets. Hence we studied the complementary question of what was the most unambiguous assembly one could obtain from a set of reads. This resulted in a rate-distortion type analysis and culminated in us developing a software called HINGE for bacterial assembly, which is used reasonably widely.
Humans and other higher organisms are diploid, that is they have two copies of their genome. These two copies are almost identical with some polymorphic sites and regions (less than 0.3% of the genome). The problem here is to estimate which of the polymorphisms are on the same copy of a chromosome from noisy observations. We studied the information limits of this problem and came up with various algorithms to solve this problem.
We considered the maximum likelihood decoding for this problem, and characterise the number of samples necessary to be able to recover through a connection to convolutional codes. We also drew connections between this problem and community detection problems and used that to derive a spectral algorithm for this.
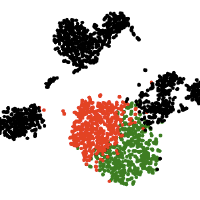
Single-cell computational pipelines involve two critical steps: organizing cells (clustering) and identifying the markers driving this organization (differential expression analysis). State-of-the-art pipelines perform differential analysis after clustering on the same dataset. We observe that because clustering forces separation, reusing the same dataset generates artificially low p-values and hence false discoveries, and we introduce a valid post-clustering differential analysis framework which corrects for this problem.
Many single-cell RNA-seq discoveries are justified using very small p-values. We observe that these p-values are often spuriously small. Existing workflows perform clustering and differential expression on the same dataset, and clustering forces separation regardless of the underlying truth, rendering the p-values invalid. This is an instance of a broader phenomenon, colloquially known as “data snooping”, which causes false discoveries to be made across many scientific domains. While several differential expression methods exist, none of these tests correct for the data snooping problem eas they were not designed to account for the clustering process. We introduce a method for correcting the selection bias induced by clustering. We attempt to close the gap between the blue and green curves in the rightmost plot by introducing the truncated normal (TN) test. The TN test is an approximate test based on the truncated normal distribution that corrects for a significant portion of the selection bias.
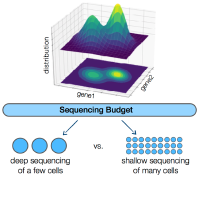
An underlying question for virtually all single-cell RNA sequencing experiments is how to allocate the limited sequencing budget: deep sequencing of a few cells or shallow sequencing of many cells? A mathematical framework reveals that, for estimating many important gene properties, the optimal allocation is to sequence at the depth of one read per cell per gene. Interestingly, the corresponding optimal estimator is not the widely-used plugin estimator but one developed via empirical Bayes.
Single-cell RNA sequencing (scRNA-Seq) technologies have revolutionized biological research over the past few years by providing us with the tools to simultaneously interrogate the transcriptional states of hundreds of thousands of cells in a single experiment. However, this seemingly unconstrained increase in the number of samples available for scRNA-Seq introduces a practical limitation in the total number of reads that can be sequenced per cell. More reads can significantly reduce the effect of the technical noise in estimating the true transcriptional state of a given cell, while more cells can provide us with a broader view of the biological variability in the population. A natural experimental design question arises; how should we choose to allocate a fixed sequencing budget across cells, in order to extract the most information out of the experiment? This question has attracted a lot of attention in the literature, but as of now, there has not been a clear answer. In this work, we develop a mathematical framework to study the corresponding trade-off and show that ~1 read per cell per gene is optimal for estimating several important quantities of the underlying distribution. Interestingly, our results indicate that the corresponding optimal estimator is not the commonly-used plug-in estimator, but the one developed via empirical Bayes (EB).
David Tse
Room 264, Packard Building
Electrical Engineering Department
350 Jane Stanford Way
Stanford, CA 94305-9515
dntse@stanford.edu
Helen Niu
Room 310, Packard Building
Electrical Engineering Department
350 Jane Stanford Way
Stanford, CA 94305-9515
Tel: (650) 723-8121
Fax: (650) 723-9251
helen.niu@stanford.edu
